Divide and conquer algorithms
Communication 1
Monday 25 November 2019 there will be the evaluation of the course
Please do not miss it!
Please, do it carefully and honestly, since it is one of the most important inputs I will have to understand what can be improved in the next year course
Communication 2
Please, in your answers to the various exercises online, if you have to write a Python code, be sure that the correct indent is preserved by previewing your post before to publish it
You can use the ``` environment for defining your Python code:
```
write your Python code here
```Communication 3
Clarifications on test-driven development
-
All the tests must be passed (i.e. they should return
True) in order to claim that an algorithm returns what it is expected -
Writing the right tests is very important since it would allow you to catch wrong behaviours of functions in presence of specific input values
However, to use only one test is not enough
Test your function by using different kinds of input, including the unusual ones, e.g. empty list, lists in which some items are repeated
Communication 4
Developing an algorithm: defining all the steps that permit to analyse and process an input and to produce some desired output according to the various situations (e.g. possibly different input values) that may happen
Running an algorithm: executing all the steps defined by an algorithm by using, as input, a particular value so as to return a specific output
Developing an algorithm
def f(n):
return n + 1Running an algorithm
f(4)Any question about the previous lecture?
Historic hero: John von Neumann

He was a computer scientist, mathematicians, and physicists
Several contribution in quantum mechanics, game theory, and self-replicating machines
Von Neumann architecture: guidelines for building physical electronic computers, included in the document written by John von Neumann for defining the main design principles of the EDVAC, the binary-based successor of the ENIAC
Immutable and mutable values
| type | immutable | mutable |
|---|---|---|
| str | x | |
| int | x | |
| float | x | |
| bool | x | |
None | x | |
| set | x | |
| dict | x | |
| tuple | x | |
| list | x | |
| deque | x |
Immutable by value
def add_one(n):
n = n + 1
return n
my_num = 41
print(my_num) # 41
result = add_one(my_num)
print(my_num) # 41
print(result) # 42Mutable by reference
def append_one(l):
l.append(1)
return l
my_list = list()
my_list.append(2)
print(my_list) # list([2])
result = append_one(my_list)
print(my_list) # list([2, 1])
print(result) # list([2, 1])Divide and conquer approach
Divide and conquer algorithm is based on four steps
[base case] address directly if it is an easy-to-solve problem, otherwise
[divide] split the input material into two or more balanced parts, each depicting a sub-problem of the original one
[conquer] run the same algorithm recursively for every balanced parts obtained in the previous step
[combine] reconstruct the final solution of the problem by means of the partial solutions
Advantages: usually quicker than brute force
Disadvantages: recursion must be defined carefully
Merge sort
Computational problem: sort all the items in a given list
Merge sort was proposed by John von Neumann in 1945
It implements a divide a conquer approach for sorting items in a list
It is more efficient than the insertion sort
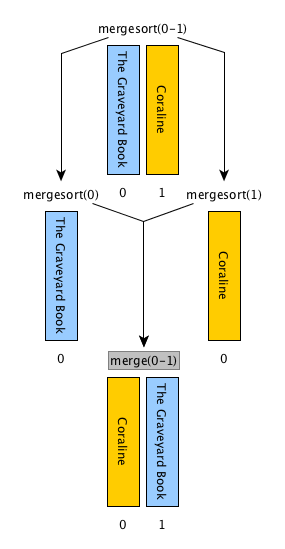
It needs an ancillary function:def merge(left_list, right_list)
It combines two ordered input lists together so as to return a new list which contains all the items in the input lists ordered
Merge: description
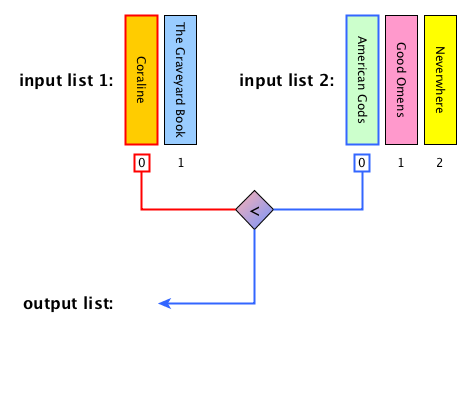
Merge: description

Merge: description
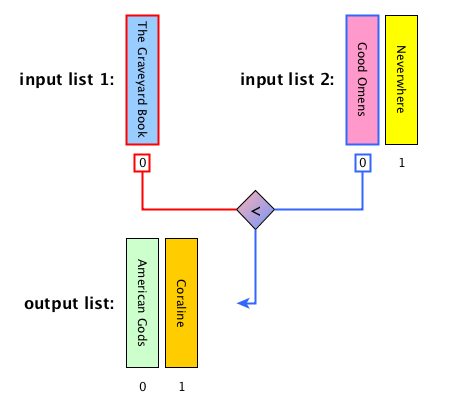
Merge: description
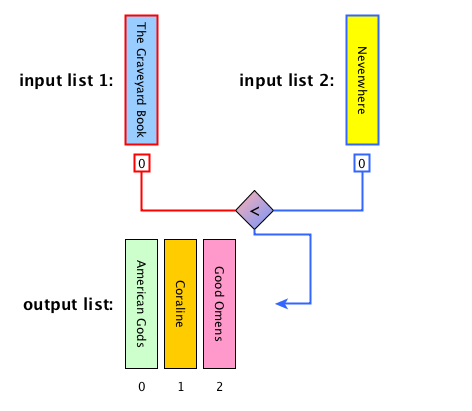
Merge: description
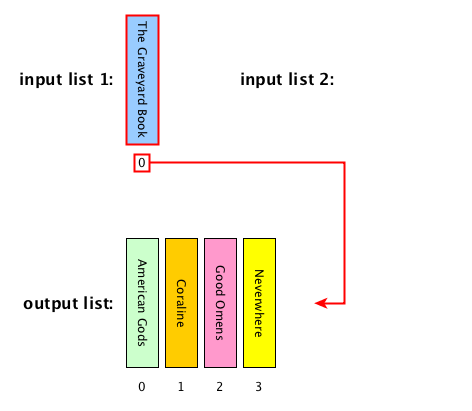
Merge: description
Merge: algorithm
def merge(left_list, right_list):
result = list()
while len(left_list) > 0 and len(right_list) > 0:
left_item = left_list[0]
right_item = right_list[0]
if left_item < right_item:
result.append(left_item)
left_list.remove(left_item)
else:
result.append(right_item)
right_list.remove(right_item)
result.extend(left_list)
result.extend(right_list)
return resultMerge sort: steps
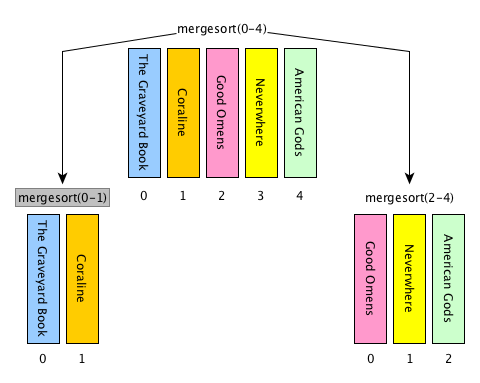
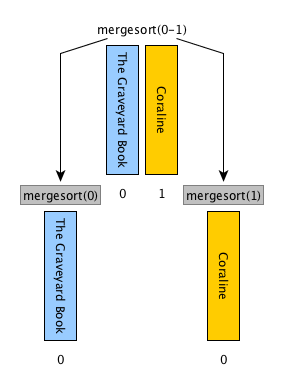
[base case] if the input list has only one item, return the list as it is, otherwise
[divide] split the input list into two balanced halves, i.e. containing almost the same number of items each
[conquer] run recursively the merge sort algorithm on each of the halves obtained in the previous step
[combine] merge the two ordered lists returned by the previous step by using
def merge(left_list, right_list)and return the result
Merge sort: description
Merge sort: description
Merge sort: description
Merge sort: description
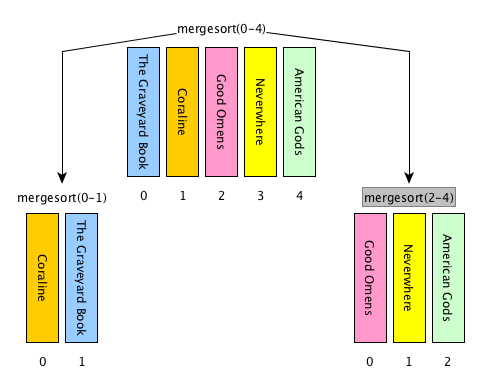
Merge sort: description
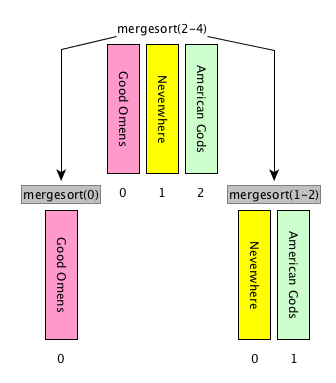
Merge sort: description
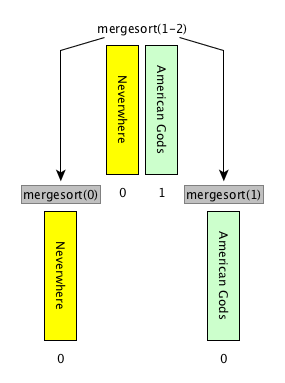
Merge sort: description

Merge sort: description
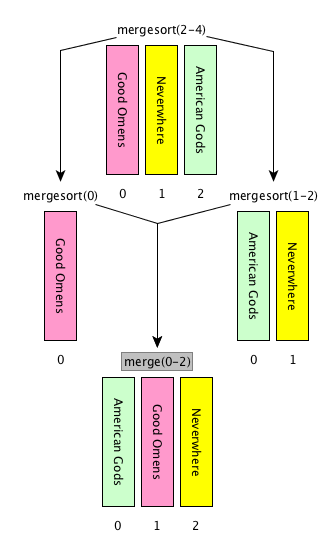
Merge sort: description
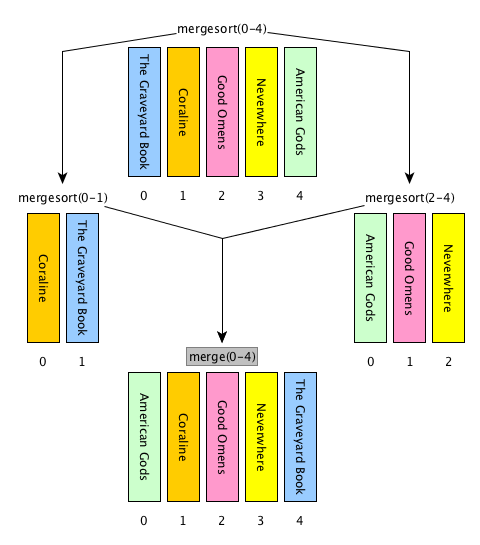
Merge sort: description
Merge sort: ancillary operations
Floor division: <number_1> // </number_2>
It returns only the integer part of the result number discarding the fractional part
E.g.: 3 // 2 = 1, 6 // 2 = 3, 1 // 4 = 0
Create sublist:
<list>[<start_position>:<end_position>]
Creates a new list containing all the items in <list> that range from <start_position> to <end_position>-1
E.g., considering my_list = list(["a", "b", "c"]), my_list[0:1] returns list(["a"]), my_list[1:3] returns list(["b", "c"])
Merge sort: algorithm
def merge_sort(input_list):
input_list_len = len(input_list)
if input_list_len <= 1:
return input_list
else:
mid = input_list_len // 2
left = merge_sort(input_list[0:mid])
right = merge_sort(input_list[mid:input_list_len])
return merge(left, right)