Computability
Any question about the previous lecture?
Historic hero: Alan Turing

Computer scientist (+ works in mathematics, logic, philosophy, and biology)
Father of Theoretical Computer Science (see Turing machine) and of Artificial Intelligence (see Turing test)
Crucial contribution in deciphering the German Nazy Enigma machine during the Second World War - he was appointed an Officer of the Order of the British Empire (OBE)
Turing machine

It is a theoretical machine
Turing machine can be used to simulate any algorithm
If you can define an algorithm for solving a particular computational problem, then there exists a Turing machine that can solve the same problem as well, and vice versa
It is composed by:
an infinite memory tape containing cells - each cell can contain 0 (blank symbol) or 1
an head for reading/writing/moving on the tape
a storage for recording the current state
a finite table of instructions + start and end states
Table of instructions
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
A |
0 or 1 |
1 |
right |
B |
B |
0 or 1 |
0 |
right |
A |
Start state: A
No end states
Graphical example
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
A |
0 or 1 |
1 |
right |
B |
B |
0 or 1 |
0 |
right |
A |
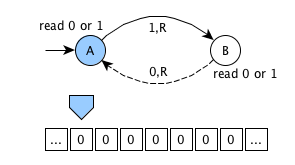
Graphical example
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
A |
0 or 1 |
1 |
right |
B |
B |
0 or 1 |
0 |
right |
A |
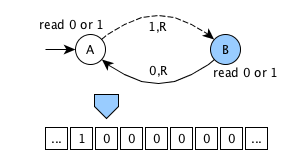
Graphical example
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
A |
0 or 1 |
1 |
right |
B |
B |
0 or 1 |
0 |
right |
A |
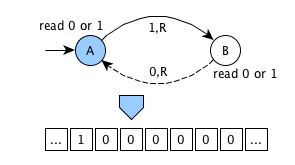
Graphical example
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
A |
0 or 1 |
1 |
right |
B |
B |
0 or 1 |
0 |
right |
A |
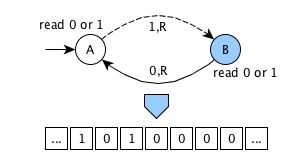
Graphical example
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
A |
0 or 1 |
1 |
right |
B |
B |
0 or 1 |
0 |
right |
A |
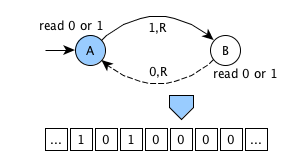
Graphical example
| Current state | Tape symbol | Write symbol | Move head | Next state |
|---|---|---|---|---|
A |
0 or 1 |
1 |
right |
B |
B |
0 or 1 |
0 |
right |
A |
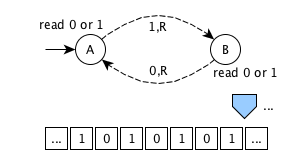
Cost of computation
The previous simple machine can compute indefinitely (there are no ending states)
Other machines could compute a result in a reasonable finite time
There can be also algorithms that must spend an exaggerated time (even if still finite) to return a result
Execution cost of an algorithm: how much time, indicatively, an algorithm needs for returning a result
How to do it
Computational complexity theory: classifying computational problems
Computational problem: a problem that be solved algorithmically by a computer
Classification to an algorithm is provided according to a specific hierarchy of classes that express the difficulty in solving such problems
Analysis of algorithms: understanding the amount of time, storage and other resources that are needed to execute such algorithm, defined in terms of a mathematical function
Typical question: how many instructions an algorithm has to execute to return the final result from that input?
Lessons to learn
The efficiency of an algorithm is directly derived and guided by the way such algorithm has been developed
It is possible to develop two different algorithms addressing the same computational problem that take two drastic different times for returning the result
Important questions
Can we use algorithms for computing whatever we want?
Alternatively, there exists a limitation on what we can compute?
Alternatively, is it possible to define a computational problem that cannot be solved by any algorithm?
Turing created his machine for answering this question
Reductio ad absurdum
One of the most used approaches to demonstrate that something cannot exist
Idea: to come to a paradoxical and self-contradictory situation in which, for instance, the existence of an algorithm contradicts its existence itself
Library paradox
Setting

Problem
Resolution


The halting problem
Proposed by David Hilbert in 1900
Description: is it possible to develop an algorithm that takes another algorithm as input and determines if such input algorithm will terminate its execution at some point or it will run forever?
From Turing point of view: can we develop a Turing machine which is able to certainly decide if another machine will terminate its execution or will not?
Resolution (part 1)
Suppose we have a does it halt
algorithm which takes in input another algorithm and returns yes if the input algorithm terminates, and no otherwise
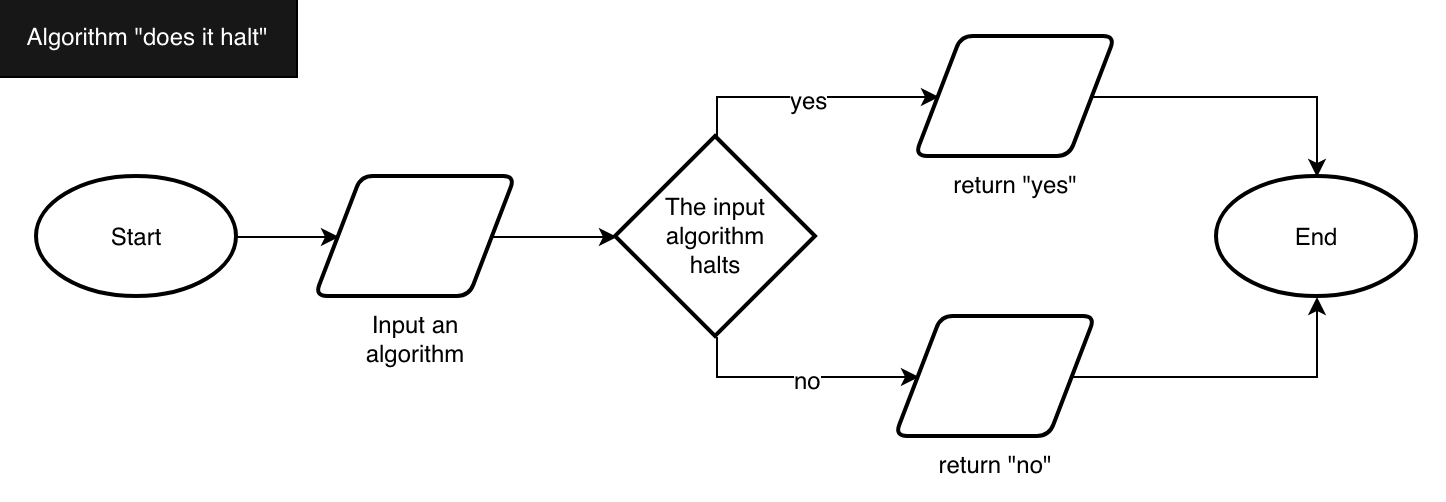
Resolution (part 2)
Reuse the does it halt
algorithm to develop a new algorithm
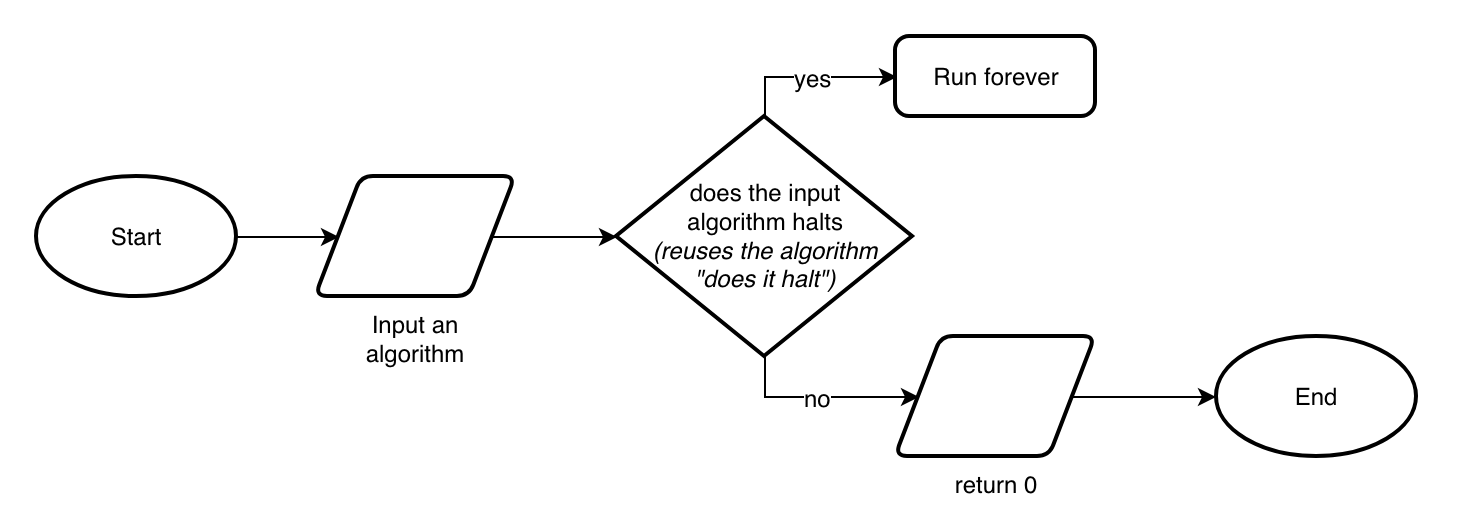
Run forever
exists since we can develop a Turing machine that does not terminate
Resolution (part 3)
What happens if we try to execute the last algorithm passing itself as input?
Two situations:
if
does it halt
says that the last algorithm stops, then such last algorithm runs foreverif
does it halt
says that the last algorithm runs forever, then such last algorithm stops
Contradiction
Whatever is the behaviour of the last algorithm, it always generates a contradiction
While the last algorithm can be developed (all the widgets in the diagram can be actually developed), then it is does it halt
that cannot be developed
Turing's machines and their analyses posed clear limits to what we can compute, since there are specific computational problems that cannot be solved