Divide and conquer algorithms
Any question about the previous lecture?
Historic hero: John von Neumann

He was a computer scientist, mathematicians, and physicists
Several contribution in quantum mechanics, game theory, and self-replicating machines
Von Neumann architecture: guidelines for building physical electronic computers, included in the document written by John von Neumann for defining the main design principles of the EDVAC, the binary-based successor of the ENIAC
Immutable and mutable values
| type | immutable | mutable |
|---|---|---|
| str | x | |
| int | x | |
| float | x | |
| bool | x | |
None | x | |
| set | x | |
| dict | x | |
| tuple | x | |
| list | x | |
| deque | x |
Immutable by value
def add_one(n):
n = n + 1
return n
my_num = 41
print(my_num) # 41
result = add_one(my_num)
print(my_num) # 41
print(result) # 42Mutable by reference
def append_one(l):
l.append(1)
return l
my_list = list()
my_list.append(2)
print(my_list) # list([2])
result = append_one(my_list)
print(my_list) # list([2, 1])
print(result) # list([2, 1])Divide and conquer approach
Divide and conquer algorithm is based on four steps
[base case] address directly if it is an easy-to-solve problem, otherwise
[divide] split the input material into two or more balanced parts, each depicting a sub-problem of the original one
[conquer] run the same algorithm recursively for every balanced parts obtained in the previous step
[combine] reconstruct the final solution of the problem by means of the partial solutions
Advantages: usually quicker than brute force
Disadvantages: recursion must be defined carefully
Merge sort
Computational problem: sort all the items in a given list
Merge sort was proposed by John von Neumann in 1945
It implements a divide a conquer approach for sorting items in a list
It is more efficient than the insertion sort
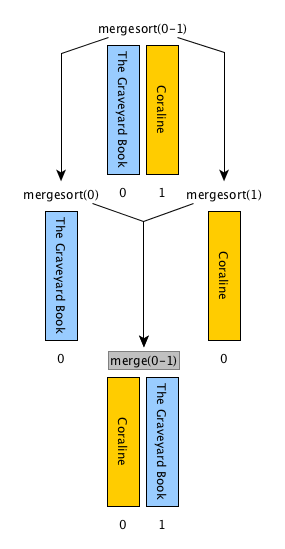
It needs an ancillary function:def merge(left_list, right_list)
It combines two ordered input lists together so as to return a new list which contains all the items in the input lists ordered
Merge: description
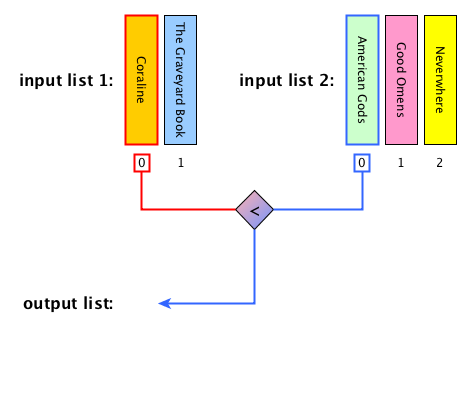
Merge: description
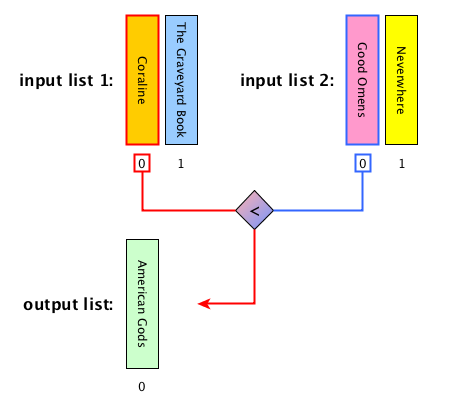
Merge: description
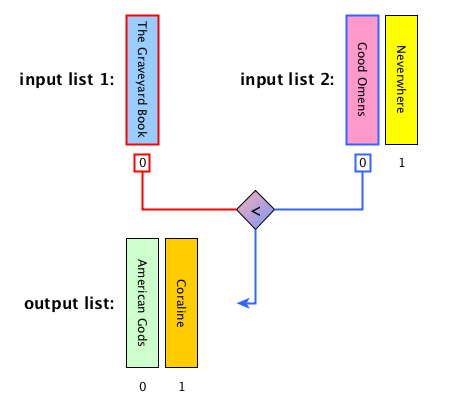
Merge: description
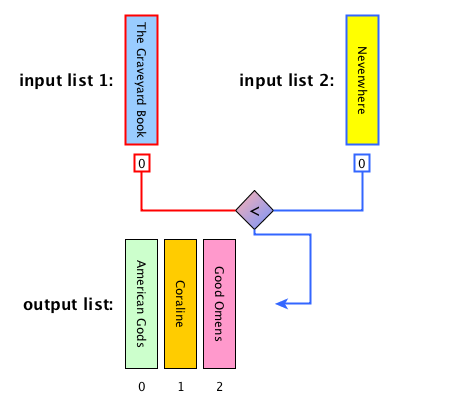
Merge: description

Merge: description
Merge: algorithm
def merge(left_list, right_list):
result = list()
while len(left_list) > 0 and len(right_list) > 0:
left_item = left_list[0]
right_item = right_list[0]
if left_item < right_item:
result.append(left_item)
left_list.remove(left_item)
else:
result.append(right_item)
right_list.remove(right_item)
result.extend(left_list)
result.extend(right_list)
return resultMerge sort: steps
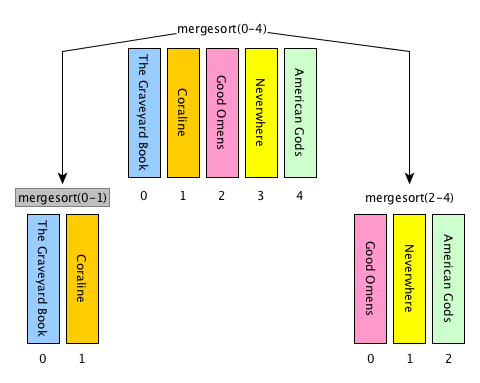
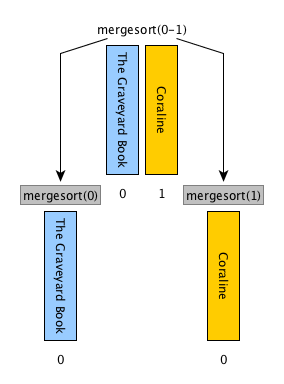
[base case] if the input list has only one item, return the list as it is, otherwise
[divide] split the input list into two balanced halves, i.e. containing almost the same number of items each
[conquer] run recursively the merge sort algorithm on each of the halves obtained in the previous step
[combine] merge the two ordered lists returned by the previous step by using
def merge(left_list, right_list)and return the result
Merge sort: description
Merge sort: description
Merge sort: description
Merge sort: description
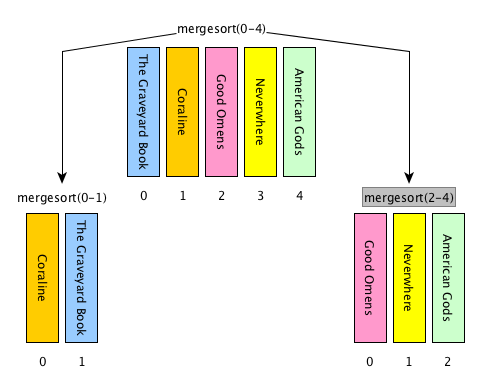
Merge sort: description
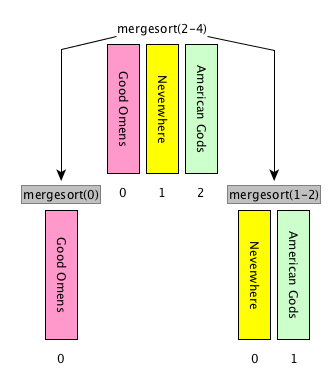
Merge sort: description
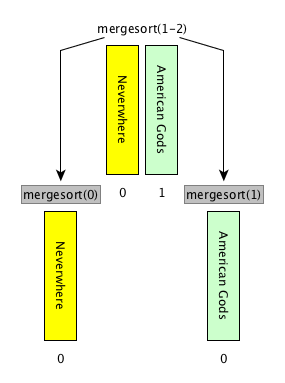
Merge sort: description
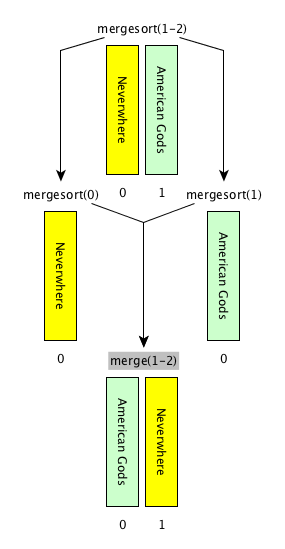
Merge sort: description
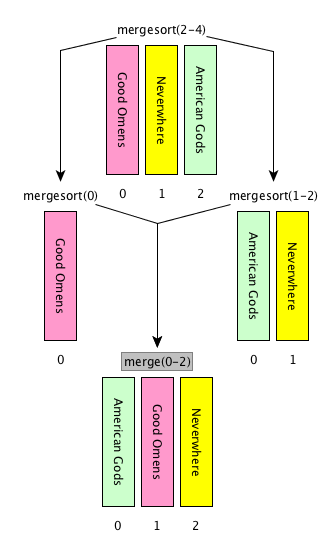
Merge sort: description
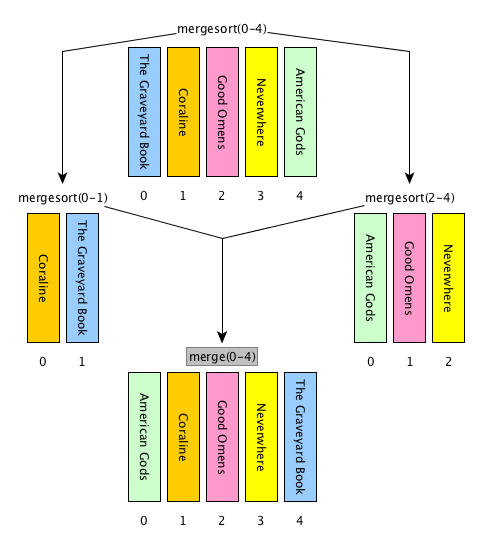
Merge sort: description
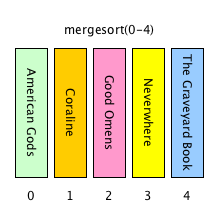
Merge sort: ancillary operations
Floor division: <number_1> // </number_2>
It returns only the integer part of the result number discarding the fractional part
E.g.: 3 // 2 = 1, 6 // 2 = 3, 1 // 4 = 0
Create sublist:
<list>[<start_position>:<end_position>]
Creates a new list containing all the items in <list> that range from <start_position> to <end_position>-1
E.g., considering my_list = list(["a", "b", "c"]), my_list[0:1] returns list(["a"]), my_list[1:3] returns list(["b", "c"])
Merge sort: algorithm
def merge_sort(input_list):
input_list_len = len(input_list)
if input_list_len <= 1:
return input_list
else:
mid = input_list_len // 2
left = merge_sort(input_list[0:mid])
right = merge_sort(input_list[mid:input_list_len])
return merge(left, right)