Dynamic programming algorithms
Communication 1
Video of previous lectures:
Communication 2
Usually, during one of the last lectures of the course, you will be asked to fill-up a questionnaire on the organisation of the course and related stuff - it is anonymous, of course
Please, do it carefully and honestly, since it is one of the most important inputs I will have to understand what can be improved in the next year course
The fact that the course of this year is slightly different from the one held during the previous year one is mainly due to the comments I have received through these questionnaires
Any question about the previous lecture?
Historic hero: Fibonacci

He was a mathematician
First person to introduce in Europe the Hindu-Arabic number system (i.e. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
Publication Liber Abaci (Book of Calculation) in 1202: how to use such numeral system for addressing situations related to commerce, and for solving generic mathematical problems
Fibonacci sequence
Fibonacci developed an infinite sequence of numbers, named after him, that described ideally the number of male-female pairs of rabbits at a given month
fib(0) = 0 [base case 1]
fib(1) = 1 [base case 2]
fib(n) = fib(n-1) + fib(n-2) [recursive step]
Fibonacci: divide and conquer
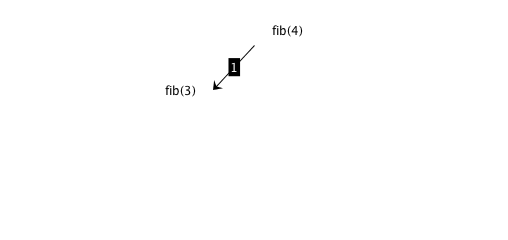
Fibonacci: divide and conquer
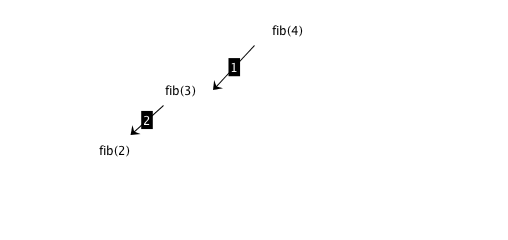
Fibonacci: divide and conquer
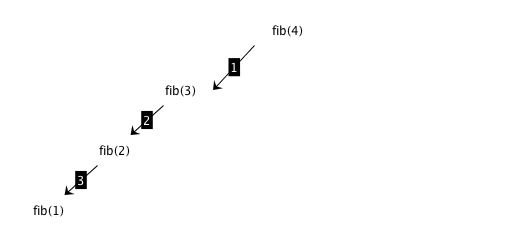
Fibonacci: divide and conquer
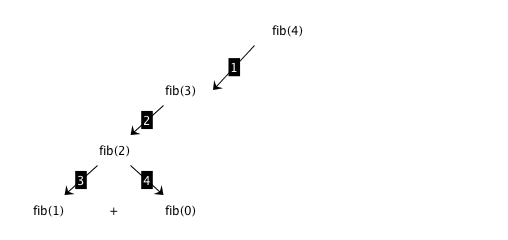
Fibonacci: divide and conquer
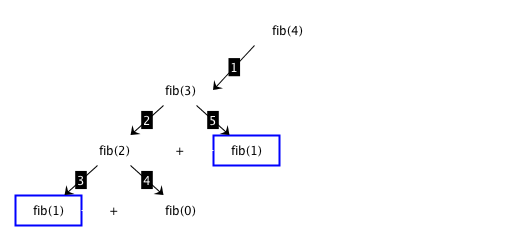
Fibonacci: divide and conquer
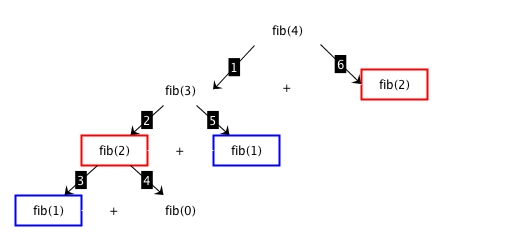
Fibonacci: divide and conquer
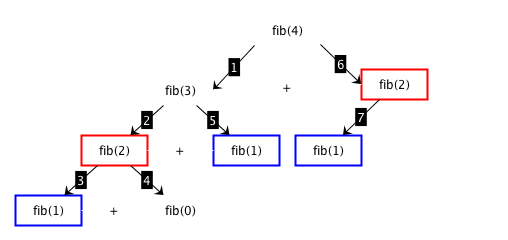
Fibonacci: divide and conquer
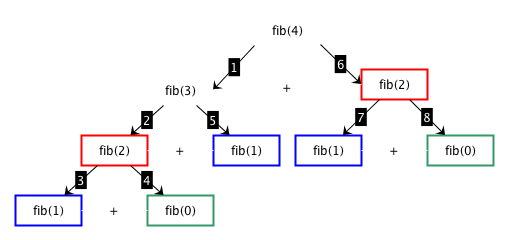
Fibonacci (divide and conquer): algorithm
def fib_dc(n):
if n <= 0:
return 0
elif n == 1:
return 1
else:
return fib_dc(n-1) + fib_dc(n-2)Dynamic programming approach
Dynamic programming algorithm is based on six steps
[base case: solution exists] return the solution calculated previously, otherwise
[base case: address directly] address directly if it is an easy-to-solve problem, otherwise
[divide] split the input material into two or more balanced parts, each depicting a sub-problem of the original one
[conquer] run the same algorithm recursively for every balanced parts obtained in the previous step
[combine] reconstruct the final solution of the problem by means of the partial solutions
[memorize] store the solution to the problem for reusing it
Fibonacci: dynamic programming
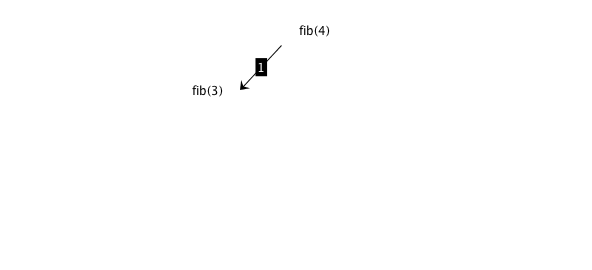
Fibonacci: dynamic programming
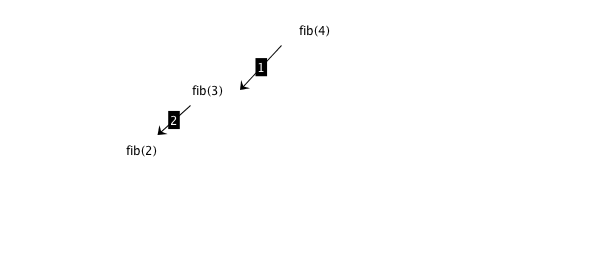
Fibonacci: dynamic programming
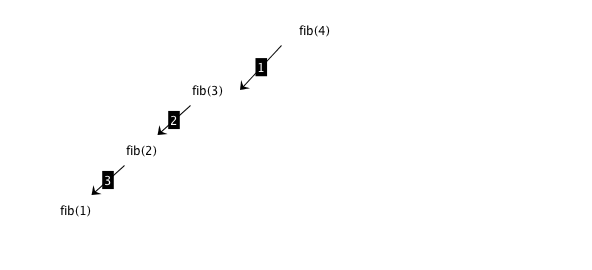
Fibonacci: dynamic programming
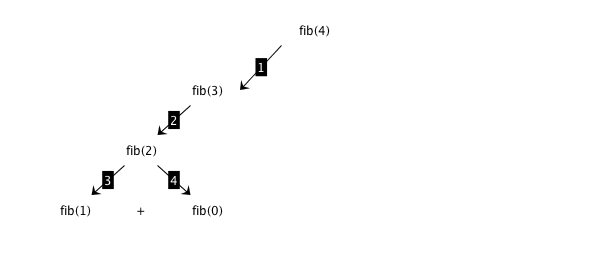
Fibonacci: dynamic programming
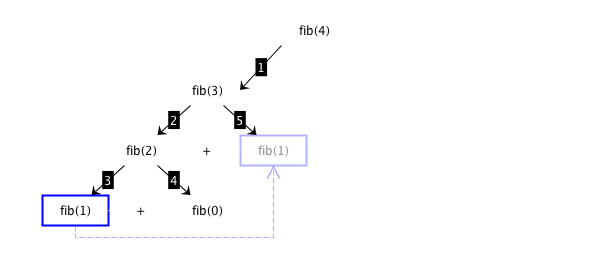
Fibonacci: dynamic programming
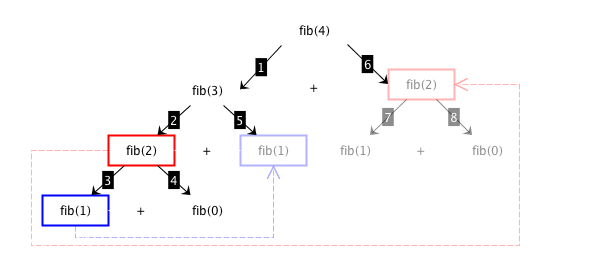
Fibonacci: ancillary operation
Non-inclusion in dictionary:
<key> not in <dictionary>
Comparison that returns True if <key> is not included as key in any pair of <dictionary>
Fibonacci (dynamic programming): algorithm
def fib_dp(n, d):
if n not in d:
if n <= 0:
d[n] = 0
elif n == 1:
d[n] = 1
else:
d[n] = fib_dp(n-1, d) + fib_dp(n-2, d)
return d.get(n)