Development - Advanced, exercise 13

Text

AtariGo is a simplified version of Go. Its rules are pretty simple. Two teams, Black and White, take turns placing a stone (game piece) of their own colour on a vacant point (intersection) of the grid on the board. Once placed, stones do not move. A vacant point adjacent to a stone is called a liberty for that stone. Connected stones formed a group and share their liberties. A stone or group with no liberties is captured. Black plays first. The first team to capture anything wins.

Suppose you want to develop a software that is able to play AtariGo on a 4x4 board, like the one shown in the figure that is already populated with some stones. And suppose we use tuples for defining every position in the board (shown on the bottom of the figure).

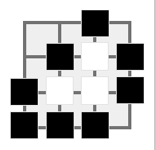
(0, 0) (1, 0) (2, 0) (3, 0)
(0, 1) (1, 1) (2, 1) (3, 1)
(0, 2) (1, 2) (2, 2) (3, 2)
(0, 3) (1, 3) (2, 3) (3, 3)

One of the functions to implement returns the set of positions of the board that are not occupied by any stone and that does not result in the stone being immediately captured if placed. Supposing White has to play in the board in the figure, such a function would return the set containing the tuples (0, 0), (1, 0) and (0, 1) – but not (3, 3) since if White places a stone there it will be immediately captured.

Write a function in Python – def get_good_white_moves(white, black) – that takes in input the set of tuples identifying the stones placed in the 4x4 board in the previous turns by the two players (white and black, respectively) and that returns the set of all the tuples identifying possible places where White can put its stone in the current turn, according to the rules mentioned above. As a simplification, avoid to check the liberties of groups of White stones.

Solution

# Test case for the function
def test_get_good_white_moves(white, black, expected):
    result = get_good_white_moves(white, black)
    if expected == result:
        return True
    else:
        return False


# Code of the function
def get_good_white_moves(white, black):
    result = set([
        (0, 0), (1, 0), (2, 0), (3, 0),
        (0, 1), (1, 1), (2, 1), (3, 1),
        (0, 2), (1, 2), (2, 2), (3, 2),
        (0, 3), (1, 3), (2, 3), (3, 3)
    ])
    result.difference_update(white)
    result.difference_update(black)

    for x, y in set(result):
        if not have_freedom((x - 1, y), black) and not have_freedom((x + 1, y), black) and \
                not have_freedom((x, y - 1), black) and not have_freedom((x, y + 1), black):
            result.remove((x, y))

    return result


def have_freedom(t, black):
    return 0 <= t[0] <= 3 and 0 <= t[1] <= 3 and t not in black


# Tests
print(test_get_good_white_moves(
    {(1, 1), (0, 2), (0, 3), (1, 0)},
    {(2, 0), (2, 1), (3, 1), (2, 2), (2, 3)},
    {(0, 0), (0, 1), (1, 2), (1, 3), (3, 2), (3, 3)}))

Additional material

The runnable Python file is available online.